原文网址:http://www.medsci.cn/article/show_article.do?id=039249e934d
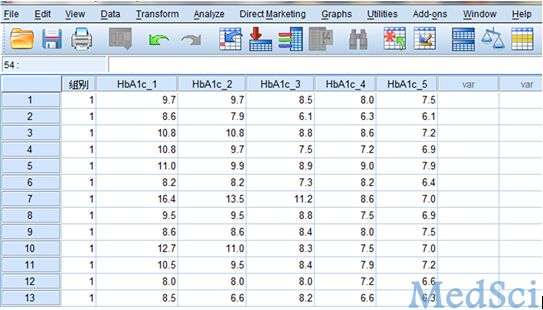
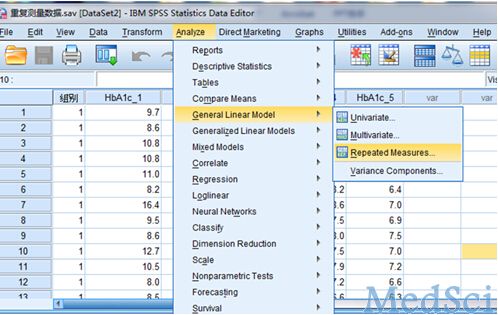
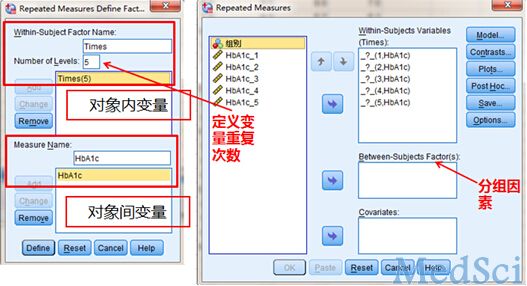
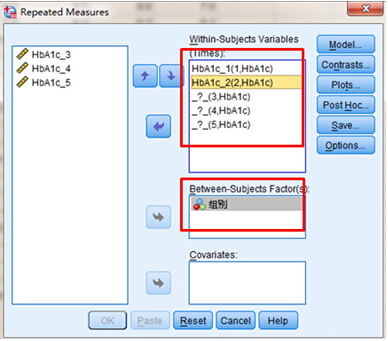
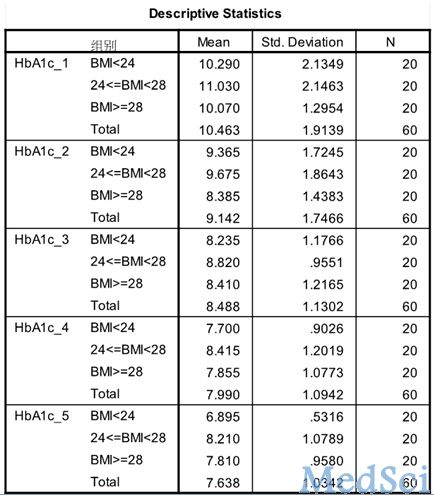
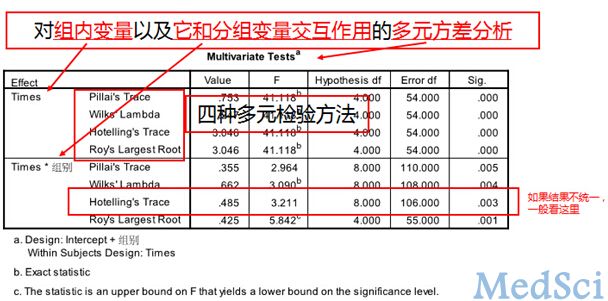
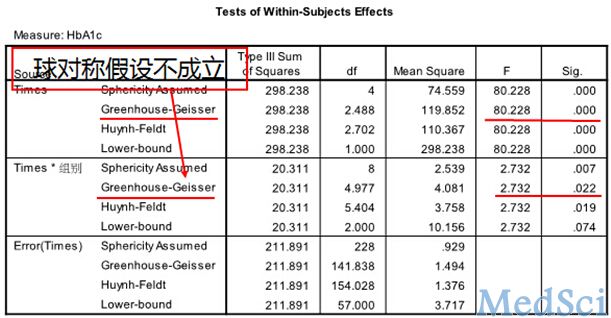
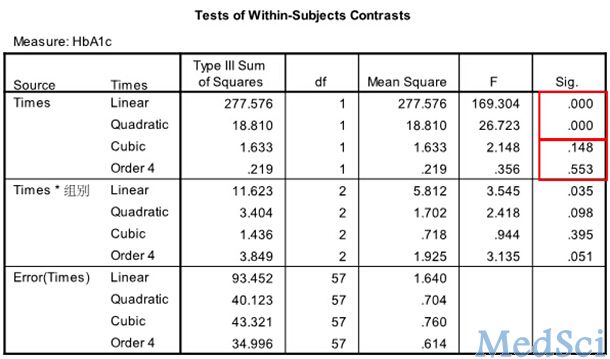
重复测量设计,即对一组或多组受试对象,在k个(k≥2)不同的时间点上,从每个人体(或样本)上重复观测同一个指标的具体取值的设计。如临床研究中,需要观察患者在不同时间的某些生理、生化或病理指标的变化趋势,或治疗干预后不同时间或疗程的疗效特点,就要进行重复测量设计。重复测量数据间存在相关性,不符合方差分析要求,所以重复测量数据资料需要采用专门的统计分析方法,该方法也是近代统计学研究的热点之一。 对于重复测量数据(临床上常称纵向监测数据),实质上每个受试对象的观察结果是多次重复测量结果的连线,统计分析的目的是比较这些连线变化趋势的特征。重复测量试验数据的方差分析需要考虑两个因素,一是处理分组,二是测量时间。可采用的统计分析方法:1. 多元方差分析方法;2. 重复测量数据的方差分析。 重复测量数据的变异由两大部分组成。一是观察对象间差异,二是重复测量间差异。观察对象间差异包括处理组间差异和观察对象个体间变异两部分;重复测量间差异包括测量时间之间差异、处理与测量时间的交互作用和组内误差三个部分。因此,重复测量数据的总变异可分解为处理组、测量时间、处理组与测量时间的交互作用、观察对象间随机误差以及重复测量误差等五个部分。 重复测量资料统计前提条件是首先要求样本是随机的,除了满足一般方差分析条件外,特别强调满足协方差阵球形性——球形检验。球形检验(Mauchly):如果P值大于α (如果α=0.05,即p>0.05),说明协方差阵的球对称性质得到满足。若球对称性得不到满足,方差分析的F值是有偏的,会增大Ⅰ类错误的概率,则需校正。否则,必须对与时间有关的F统计量的分子和分母自由度进行调整,减少Ⅰ类错误的概率。调整系数为:ε(epsilon)。 SPSS操作示例