一、问题与数据

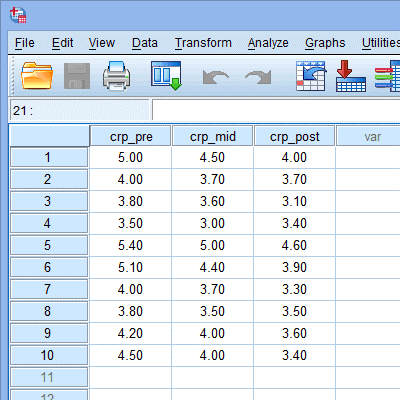
研究者招募了10名研究对象，研究对象进行了6个月的锻炼干预。CRP浓度共测量了3次：干预前的CRP浓度——crp_pre；干预中（3个月）——crp_mid；干预后（6个月）——crp_post。这三个时间点代表了受试者内因素“时间”的三个水平，因变量是CRP的浓度，单位是mg/L。部分数据如下：

二、对问题的分析

使用One-way Repeated Measures Anova进行分析时，需要考虑6个假设。 

对研究设计的假设：

假设1：因变量唯一，且为连续变量；

假设2：受试者内因素（Within-Subject Factor）有3个或以上的水平。

注：在重复测量的方差分析模型中，对同一个体相同变量的不同次观测结果被视为一组，用于区分重复测量次数的变量被称为受试者内因素，受试者内因素实际上是自变量。

对数据的假设：

假设3：受试者内因素的各个水平，因变量没有极端异常值；

假设4：受试者内因素的各个水平，因变量需服从近似正态分布；

假设5：对于受试者内因素的各个水平组合而言，因变量的方差协方差矩阵相等，也称为球形假设。

三、思维导图

(点击图片可查看大图)

四、对假设的判断

在分析时，如何考虑和处理这5个假设呢？

由于假设1-2都是对研究设计的假设，需要研究者根据研究设计进行判断，所以我们主要对数据的假设3-5进行检验。

(一) 检验假设3和假设4的SPSS操作

1. 在主菜单点击Analyze > Descriptive Statistics > Explore…，如下图：

 

2. 出现Explore对话框，将crp_pre、crp_mid和crp_post选入Dependent List，点击Plots；

 

3. 出现下图Plots对话框；

 

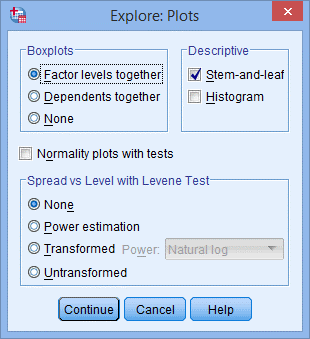
4. 在Boxplots下选择Dependents together，去掉Descriptive下Stem-和-leaf，选择Normality plots with tests，点击Continue；

 

5. 回到Explore主对话框，在Display下方选择Plots，点击OK。

 

(二) 检验假设3：受试者内因素的各个水平，因变量没有极端异常值

1. 在输出的结果中，如下图所示，在箱式图中，距离箱子边缘超过1.5倍箱身长度的数据点定义为异常值，在本例中，未发现异常值。

2. 为了方便进一步的理解，下面图示是有异常值的箱式图，上下边缘超过1.5倍箱式长度为异常值，如下图所示，用“圆圈”表示，右上标为异常值在数据表中所对应的行数；将距离箱子边缘超过3倍箱身长度的数据点定义为极端值（极端异常值），用“*”表示，右上标代表异常值在数据表中所对应的行数。因此，在箱式图中查看异常值时，可以直接看“圆圈”或“*”。

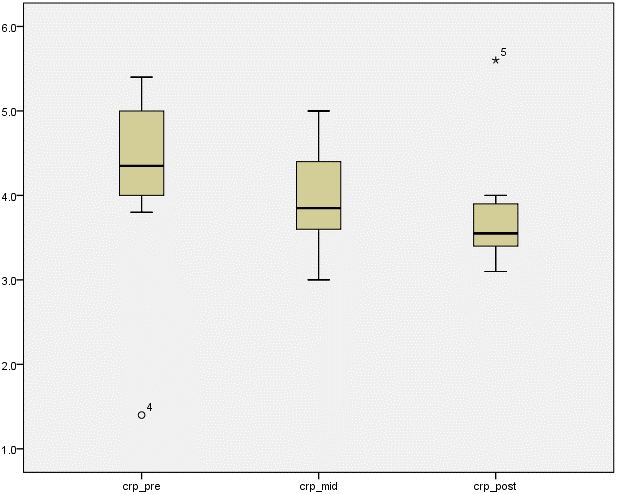
3. 异常值的处理

导致数据中存在异常值的原因有3种：

(1) 数据录入错误：首先应该考虑异常值是否由于数据录入错误所致。如果是，用正确值进行替换并重新进行检验；

(2) 测量误差：如果不是由于数据录入错误，接下来考虑是否因为测量误差导致（如仪器故障或超过量程），测量误差往往不能修正，需要把测量错误的数据删除；

(3) 真实存在的异常值：如果以上两种原因都不是，那最有可能是一种真实的异常数据。这种异常值不好处理，但也没有理由将其当作无效值看待。目前它的处理方法比较有争议，尚没有一种特别推荐的方法。

需要注意的是，如果存在多个异常值，应先把最极端的异常值去掉后，重新检查异常值情况。这是因为有时最极端异常值去掉后，其他异常值可能会回归正常。

异常值的处理方法分为2种：

(1) 保留异常值：

• 采用非参数Friedman test检验；
• 用非最近端的值代替极端异常值（如用第二大的值代替极端异常值）；
• 因变量转换成其他形式；
• 将异常值纳入分析，并坚信其对结果不会产生实质影响。

(2) 剔除异常值：

直接删除异常值很简单，但却是没有办法的办法。当我们需要删掉异常值时，应报告异常值大小及其对结果的影响，最好分别报告删除异常值前后的结果。而且，应该考虑有异常值的个体是否符合研究的纳入标准。如果其不属于合格的研究对象，应将其剔除，否则会影响结果的推论。

（更多阅读：怎么判别我的数据中存在特异值？教你几招！）

(三) 检验假设4：受试者内因素的各个水平，因变量需服从近似正态分布

1. 对于样本量较小（<>P<>P均大于0.05，说明受试者内因素的三个水平crp_pre、crp_mid和crp_post均服从正态分布。

 

2. 如果数据不服从正态分布，可以有如下4种方法进行处理：

(1) 数据转换：对转换后呈正态分布的数据进行单因素方差分析。当各组因变量的分布形状相同时，正态转换才有可能成功。对于一些常见的分布，有特定的转换形式，但是对于转换后数据的结果解释可能比较复杂。

(2) 使用非参数检验：可以使用Friedman test等非参数检验方法，但是要注意Friedman test和单因素重复测量方差分析的无效假设和备择假设不太一致。

(3) 直接进行分析：由于单因素重复测量方差分析对于偏离正态分布比较稳健，尤其是在各组样本量相等或近似相等的情况下，而且非正态分布实质上并不影响犯I型错误的概率。因此可以直接进行检验，但是结果中仍需报告对正态分布的偏离。

(4) 检验结果的比较：将转换后和未转换的原始数据分别进行单因素重复测量方差分析，如果二者结论相同，则再对未转换的原始数据进行分析。

五、SPSS操作

(一) 单因素重复测量方差分析的操作

1. 在主菜单下点击Analyze > General Linear Model > Repeated measures…，如下图所示：

2. 出现Repeated Measures Define Factor(s)对话框，如下图所示：

 

3. 在Within-Subject Factor Name:中将“factor1”更改为time，因为共测量了3次CRP的水平，所以在Number of Levels：中填入3；

4. 点击Add，出现下图：

5. 在Measure Name:中赋予因变量一个合理的名字，本例中因变量为CRP的水平，所以填入CRP，点击下方的Add，出现下图：

 

6. 点击Define，出现下图Repeated Measures对话框：

 

7. 如下图所示，Within-Subjects Variables后面的括号内是受试者内因素的名字，框内三条分别代表“time”对应的各个水平；

 

8. 将crp_pre、crp_mid和crp_post一起选入右侧的框中，如下图所示：

 

9. 点击Plots，出现Repeated Measures: Profile Plots 对话框，如下图所示：

 

10. 将time选入Horizontal Axis：框中；

 

11. 点击Add，出现下图，点击Continue；

 

12. 点击Options，出现Repeated Measures: Options对话框；

 

13. 将time选入Display Means for：中；下方Compare main effects为勾选状态；在Confidence interval adjustment：下选择Bonferroni；在Display下方勾选Descriptive statistics 和Estimates of effect size；点击Continue，点击OK。

 

(二) 单因素重复测量方差分析→自定义组间比较（custom contrasts）

如果只关心特定组别间的差异，你需要知道如何进行自定义比较（custom contrasts），以及如何对多重比较结果进行调整，这就要用到SPSS软件中的Syntax Editor窗口编写相应程序语句。当满足方差齐性条件时，推荐采用单因素重复测量方差分析进行自定义组间比较。

1. 操作同上述1-13步的操作，这里不再赘述。接下来：

(1) 点击Paste，出现IBM SPSS Statistics Syntax Editor窗口：

 

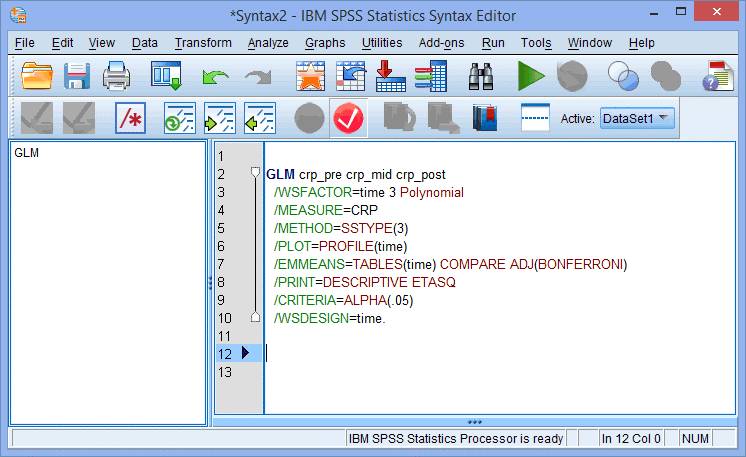
(2) 在 /PRINT 和 /CRITERIA两行中间，输入/MMATRIX = ‘0 vs 6 Months’ ALL 1 0 -1; 

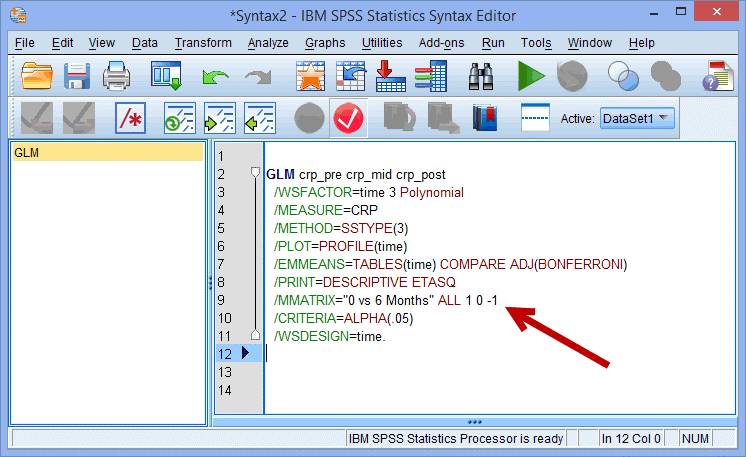
/MMATRIX=旨在告诉SPSS我们要做一个自定义假设； 1  0  -1表示要进行比较的自变量组别，组别的顺序和SPSS里输入的组别顺序有关：这里从左到右（1  0  -1）分别对应着crp_pre、crp_mid和crp_post，表示将crp_pre与crp_post进行比较。“ALL”代表受试者内因素的所有水平。

注：自定义比较包括了简单比较（simple contrasts）和复合比较（complex contrasts）。简单比较为只比较自变量某两个组别间的差异，需要建立线性比较函数（linear contrast，φ）。它包含一系列组别和每个组别对应的均数，组别取值只能为1，-1，0。我们把要比较的两组的组别分别赋值为1和-1，其他不比较的组别组别赋值为0。

本例中crp_pre组别为1，crp_post组别为-1，其他组别均为0，则是要比较干预前CRP水平和干预后CRP水平的差异，看二者的平均CRP水平的差值是否为0（即组别为1的组别减去组别为-1的组别，以组别为-1的组别为参照组，组别赋值的正负与研究设计和研究假设有关）。

(3) 用/MMATRIX指令增加另外比较：

 /MMATRIX = ‘0 vs 3&6 Months’ ALL 1 -1/2 -1/2

 

注：复合比较为比较自变量超过2个组别的组合间的差异。同样采用线性比较函数的方法，某组合的组别赋值为1或-1除以组合内的组数，但是要保证要比较的组间组合与另一组（组合）的所有组别加起来为0，组别赋值的正负与研究设计和研究假设有关。

本例中， /MMATRIX = ‘0 vs 3&6 Months’ ALL 1 -1/2 -1/2表示crp_pre与crp_mid、crp_post差异的比较。 

(4) 多重比较的校正

接下来，我们需要校正显著性水平（α），通常也可以校正每次比较的P值和可信区间，得到调整后P值和联合可信区间（simultaneous confidence intervals）。我们首先采用Bonferroni方法对显著性水平α进行校正，公式如下：

调整后α=调整前α ÷ 比较的次数

本例中我们需要进行2次比较，则调整后α=0.05÷2=0.025。

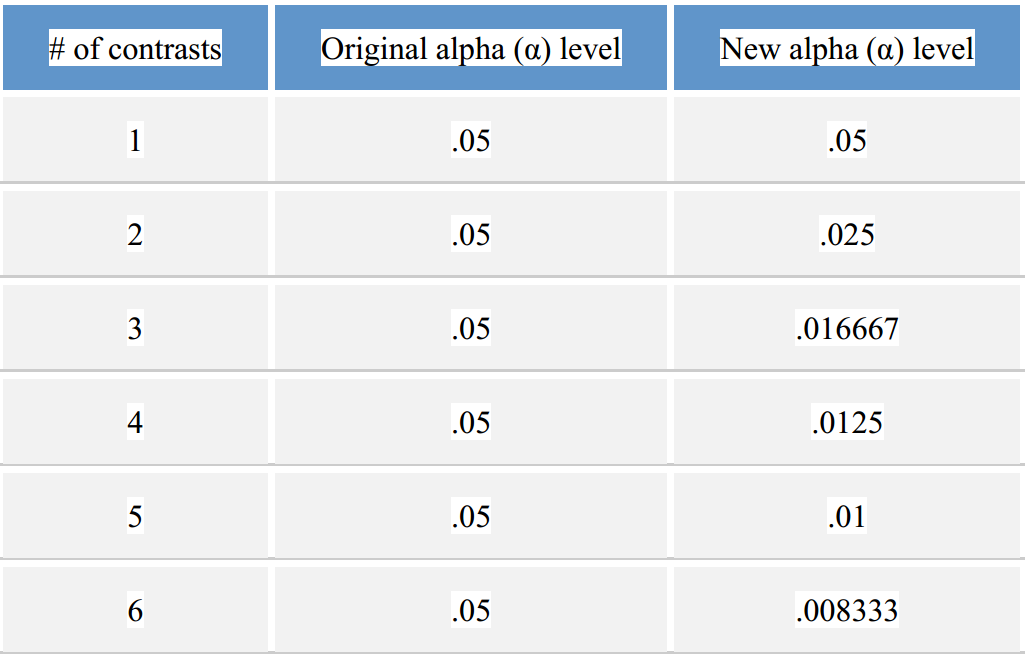
(5) 箭头标注处为SPSS软件默认的显著性水平α=0.05：

/CRITERIA=ALPHA(.05)

我们将其改为调整后的显著性水平α=0.025：

/CRITERIA=ALPHA(.025)

(6) 在菜单栏点击Run > All。

六、结果解释 

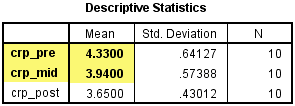
1. 基本描述

(1) SPSS首先会给出Within-Subjects Factors表，该表提示了受试者内因素crp_pre、crp_mid和crp_post对应的标签为1、2和3，在后面的Estimates表和Pairwise Comparisons表中会用到。

 

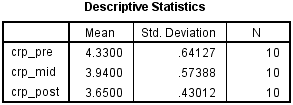
(2) Descriptive Statistics表给出了crp_pre、crp_mid和crp_post的均值、标准差和例数。受试者干预前、干预中和干预后的CRP浓度分别为4.33 ± 0.64 mg/L、3.94 ± 0.57 mg/L和3.65 ± 0.43mg/L。

 

(3) Estimates表中没有再出现crp_pre、crp_mid和crp_post的变量名，而是给出了对应的3个时间点的标签。该表中给出了crp_pre、crp_mid和crp_post的均值、标准误和95%的置信区间。

 

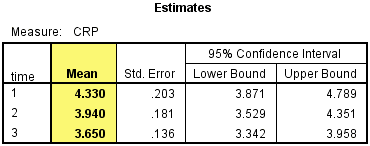
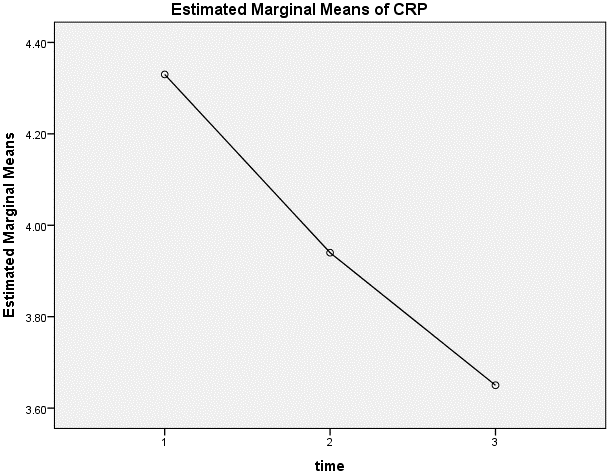
(4) Estimated Marginal Means of CRP给出了三个时间点CRP的均值的折线图，可以看到从干预前到干预后呈下降趋势，但1到2的时间点下降程度比2到3的下降程度大。

 

2. 球形假设的检验结果

(1) 在Mauchly’s Test of Sphericity表中，给出了球形假设的检验结果。如果P<>P>0.05，则满足球形假设。本例中，χ²=6.270，P=0.043，所以不满足球形假设。

 

(2) 当违背了球形假设条件时，需要进行epsilon (ε)校正。如下图突出显示，SPSS共用了三种方法进行校正，分别为：Greenhouse-Geisser、Huynh-Feldt 和Lower-bound。

在实际应用中，只用Greenhouse-Geisser和Huynh-Feldt两种方法，这两种方法计算的epsilon (ε)的值越低，说明违反球形假设的程度越大，当epsilon (ε)=1时，说明完美的服从了球形假设。

Maxwell & Delaney (2004)建议当epsilon (ε)<0.75时，使用greenhouse-geisser方法校正。其他统计学家建议当epsilon (ε)=””>0.75时，使用Huynh-Feldt方法校正。

 

(3) 满足球形假设的结果

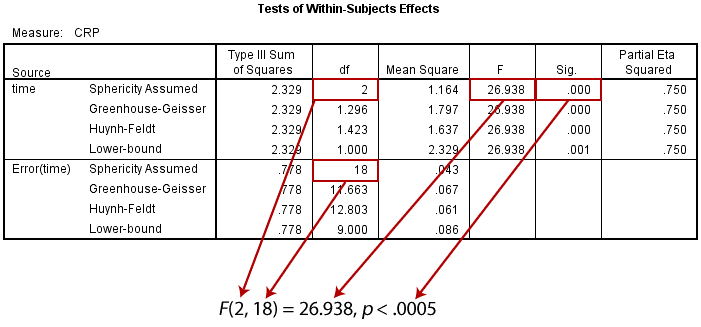
在Tests of Within-Subjects Effects表中，该表给出了crp_pre、crp_mid和crp_post在不同时间点的均值是否存在差异；偏η²（Partial Eta Squared）表示控制了其他自变量后，因变量被某一自变量解释的百分比（单因素方差分析时，即自变量对因变量的解释程度），代表样本的效应量。

如果P>0.05，则表示各组间均数差异无统计学意义（本例中，P值显示为0.000，不代表P值实际为0，而是表示P<>P<>²=0.75。

 

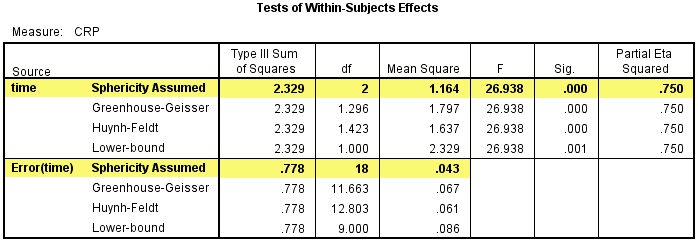
以上具体结果见下表：

 

目前许多杂志要求除了列出上述结果，还要报告效应量。计算单因素方差分析的效应量有很多方法，比较推荐的是计算偏ω²，公式如下：

 

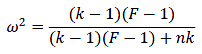
公式里k =受试者内因素的个数，F为F统计量，n=研究对象的数量，计算结果如下：

 

可见偏ω²=0.63<>²，与偏η²相比，偏ω²还考虑了抽样误差，可以提供相对准确的总体效应量的估计。

 

(4) 不满足球形假设的结果

当不满足球形假设时，可以采用Greenhouse & Geisser方法进行校正，如下表中突出显示的内容。可见，自由度（df）由原来符合球形假设时的2变成了1.296，均方（Mean Square）由原来的1.164变成1.797，方差不变。

Greenhouse & Geisser的校正结果显示不同的时间点的CRP浓度的差异具有统计学意义，F（1.296, 11.663）=26.938，P<>²=0.75。

 

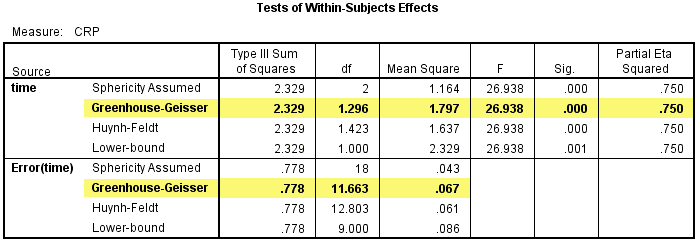
以上具体结果见下表：

 

(5) Bonferroni post hoc test检验结果

如果事前没有对特定组间差异进行假设，或者关心所有组间的两两比较，则应该进行所有组间的两两比较（post hoc test）。推荐使用Bonferroni post hoc test方法进行组间两两比较。该检验不仅提供了每两个组间比较的P值，也给出了均数差值的可信区间。

在前面我们已经知道球形假设不容易满足，会影响单因素重复测量方差分析的结果。Bonferroni post hoc test 的实质是在进行Bonferroni对显著性水平校正的基础上，配对t检验的多重比较。结果见Pairwise Comparisons表格：

 

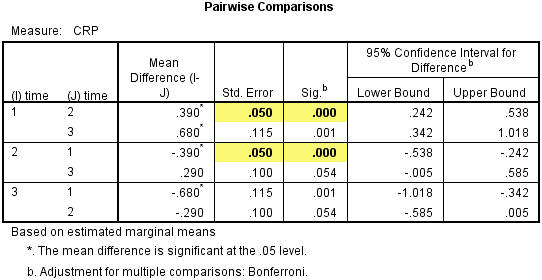
本例中受试者内因素有3个，因此会有3种不同的组间组合。当我们要比较crp_pre和crp_mid时，可以见如下标黄部分。两行均为crp_pre和crp_mid比较的结果。

 

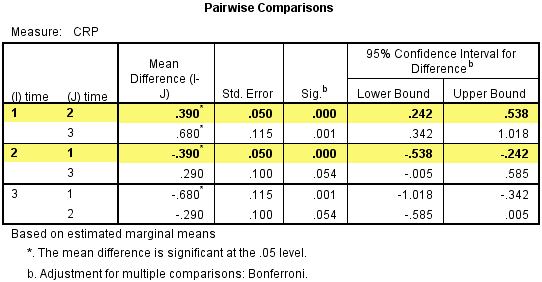
我们回顾一下之前的结果，可见上表中第一行标黄部分Mean Difference（I-J）为crp_pre与crp_mid之差：4.3300 – 3.9400 = 0.390。而第二行的标黄部分则为crp_mid与crp_pre之差： 3.9400 – 4.3300 = -0.390。

 

另外，见下图标黄部分，可见标准误和P值是相同的。

 

我们再对比一下95%的置信区间，见下表中标黄部分，置信区间的上限和下限符号不同，绝对值相同。

 

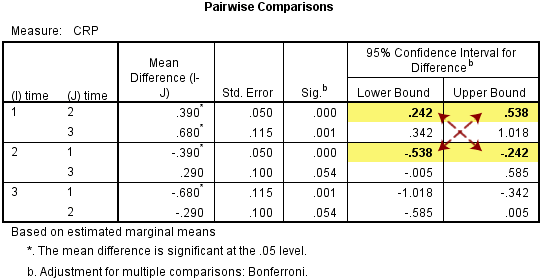
通过对上述数值的理解，我们可以报告以上结果：干预前CRP浓度为4.33 ± 0.64mg/L，干预中三个月时CRP浓度为3.94 ± 0.57mg/L，比干预前显著降低了0.390（95%置信区间：0.242-0.538）mg/L（P<0.001）,干预后6个月时crp浓度为3.65 ±=””>P=0.001），未发现干预中和干预后CRP浓度的差异具有统计学意义。

1) 自定义组间比较的结果

当我们在syntax编辑器输入了自定义比较的组别后，我们会得到如下Contrast Results (K Matrix) 表格。此表为干预前和干预后CRP浓度比较的结果，与我们当时输入的比较顺序对应一致。

 

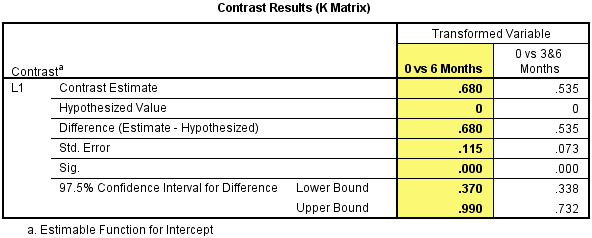
首先，我们来看Contrast Estimate、Lower Bound和Upper Bound这三行的结果。Contrast Estimate一行结果为0.680，这是所比较的2组间的均数差值；而我们看到置信区间是97.5%置信区间而非95%置信区间，这是因为我们进行了Bonferroni校正，我们还是报告成95%的置信区间。

 

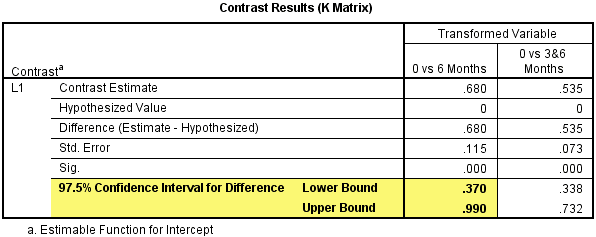
对于P值，我们双击P值，出现下图，由于进行了Bonferroni校正，显著性水平为0.025，0.000229<>

 

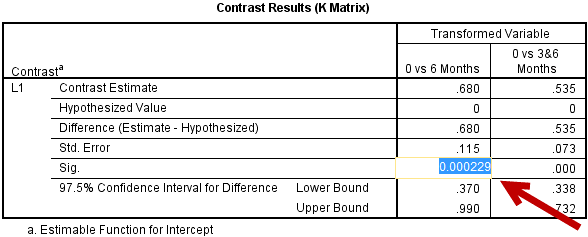
另外，还需要报告效应量，在Univariate Test Results中，偏η²=0.795。

 

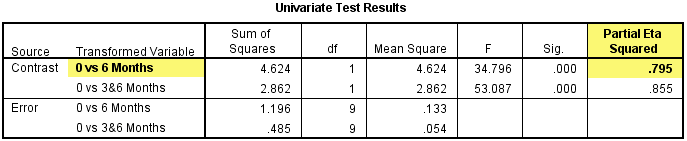
2) 复合比较的结果

如下图标黄部分所示，是干预前和干预中、干预后两者的平均值进行比较，干预前与干预中、干预后二者均值的差值为0.535（95%置信区间：0.338-0.732）mg/L，P<><>

 

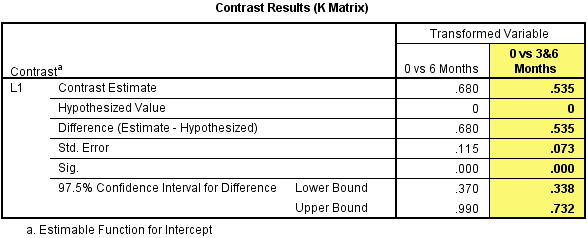
另外，还需要报告效应量，在Univariate Test Results中，偏η²=0.855。

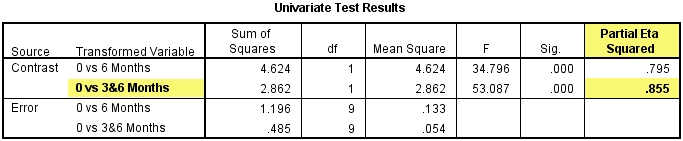
七、撰写结论

1. 假如：满足球形假设，单因素重复测量方差分析显示组间差异无统计学意义：

采用单因素重复测量方差分析方法，判断6个月的锻炼干预对受试者CRP浓度的影响。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Mauchly’s球形假设检验，因变量的方差协方差矩阵相等，χ²(2)=3.343, P=0.188。

数据以均数±标准差的形式表示。受试者干预前、干预中和干预后的CRP浓度分别为4.33 ± 0.64 mg/L、3.94 ± 0.57 mg/L和3.65 ± 0.43mg/L。干预前、干预中和干预后的CRP浓度差异不具有统计学意义，F(2, 18)=1.256, P=0.309，偏η²=0.02。

2. 假如：不满足球形假设，单因素重复测量方差分析显示组间差异无统计学意义：

采用单因素重复测量方差分析方法，判断6个月的锻炼干预对受试者CRP浓度的影响。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Mauchly’s球形假设检验，因变量的方差协方差矩阵不相等，χ²(2)=6.270, P=0.043，通过Greenhouse & Geisser方法校正ε=0.648。

数据以均数±标准差的形式表示。受试者干预前、干预中和干预后的CRP浓度分别为4.33 ± 0.64 mg/L、3.94 ± 0.57 mg/L和3.65 ± 0.43mg/L。干预前、干预中和干预后的CRP浓度差异不具有统计学意义，校正后F(1.296, 11.663)=1.256, P=0.300，偏η² =0.02。

3. 不满足球形假设，单因素重复测量方差分析显示组间差异有统计学意义，并进行了两两比较（本文例子的结果）：

采用单因素重复测量方差分析方法，判断6个月的锻炼干预对受试者CRP浓度的影响。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Mauchly’s球形假设检验，因变量的方差协方差矩阵不相等，χ²(2)=6.270, P=0.043，通过Greenhouse & Geisser方法校正ε=0.648。

数据以均数±标准差的形式表示。受试者干预前、干预中和干预后的CRP浓度分别为4.33 ± 0.64 mg/L、3.94 ± 0.57 mg/L和3.65 ± 0.43mg/L。干预前、干预中和干预后的CRP浓度差异具有统计学意义，校正后F(1.296, 11.663)=26.938, P<0.001,>²=0.75。

干预中三个月时CRP浓度比干预前显著降低了0.390（95%置信区间：0.242-0.538）mg/L（P<0.001）,干预后6个月时crp浓度比干预前显著降低了0.680（95%置信区间：0.342-1.018）mg>P=0.001），未发现干预中和干预后CRP的浓度存在的差异具有统计学意义。

4. 从无效假设和备择假设的角度出发，当单因素重复测量方差分析显示组间差异有统计学意义时：各组间均数差异有统计学意义（P<>

5. 从无效假设和备择假设的角度出发，当单因素重复测量方差分析显示组间差异无统计学意义时：各组间均数差异无统计学意义（P>0.05）。因此，不能拒绝无效假设，不能接受备择假设。

八、绘制图表

最后，我们来学习如何在SPSS软件中绘制简单线图，从而更好地展示展示单因素重复测量方差分析的结果，使其更适合于学术发表。

1. 绘制简单线图的操作

(1) 在菜单栏中，点击Graphs > Chart Builder…：

 

出现如下Chart Builder对话框：

 

(2) 在Chart Builder对话框的左下角，Choose from:模块中选择“Line”：

 

(3) 在Chart Builder对话框的中下部，出现2个不同的线图选项，把左侧的第一个（Simple Line）拖进上面的主要图表预览窗口，并点击Element Properties：

(4) 出现下图，图表预览窗口的线图横纵轴分别显示“X-Axis?”和“Y-Axis?”：

 

(5) 从Variables:模块中把自变量time拖进“X-Axis?”，把因变量crp拖进“Y-Axis?”：

 

(6) 在Element Properties对话框中勾选Display error bars，激活–Error Bars Represent– 模块，勾选Confidence intervals，Level (%):设定为95，当然也可以根据需要勾选Standard error或者Standard deviation，点击Apply：

 

(7) 在’Edit Properties of: 模块中点击’Y-Axis1 (Line1)’进行设置，出现下图：

 

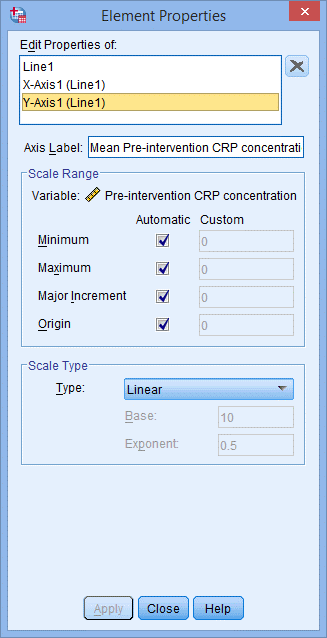
(8) 去掉勾选Scale Range下的Minimum，点击Apply并进行确认；

 

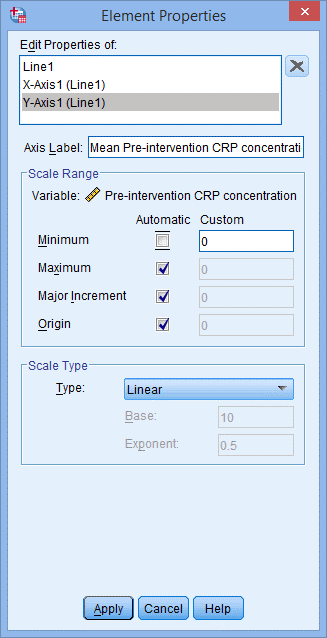
(9) 如果想改变自变量分组的顺序，可以在’Edit Properties of: 模块中点击’X-Axis1 (Line1)’进行设置，并在更改后点击Apply，点击OK。

 

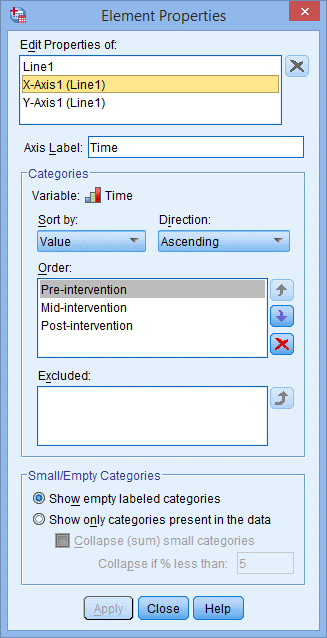
2. 简单线图结果

按照上述操作步骤，生成简单线图如下图所示：error bar表示均值的95%置信区间。