1. 单条剂量-反应曲线
让我们看看如何使用包中的训练数据集拟合剂量 – 反应曲线。drc
library(drc)在曲线拟合之前,了解数据的外观非常重要。下面,我们在原始尺度和对数尺度上创建一个具有 x 变量的绘图。
head(ryegrass,3)
## rootl conc
## 1 7.580000 0
## 2 8.000000 0
## 3 8.328571 0
op <- par(mfrow = c(1, 2), mar=c(3.2,3.2,2,.5), mgp=c(2,.7,0)) #make two plots in two columns
plot(rootl ~ conc, data = ryegrass, main="Original Dose Scale")
plot(rootl ~ log(conc+.1), data = ryegrass, main="Logarithmic Dose Scale")
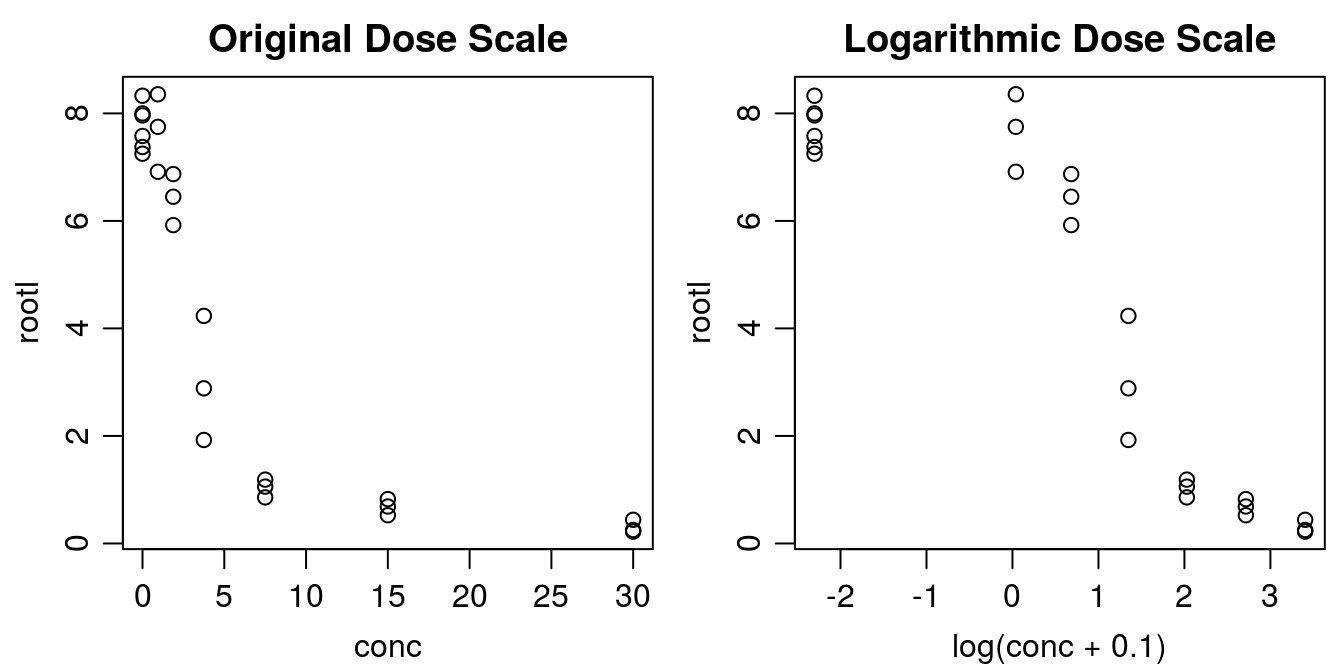
图 1:绘制剂量反应数据的方法有两种,drc 包中的默认设置是使用 x 的对数刻度。请注意,对于对数剂量刻度,未定义未处理的对照 0。这就是为什么我们在取对数之前将0.1添加到浓度中。
下面我们拟合一个具有用户定义参数名称的四参数 log-logistic 模型。函数中包含的参数(b、c、d 和 e)的默认名称对许多杂草科学家可能没有意义,但该参数可用于促进与经验不足的用户共享输出。四参数对数-逻辑曲线有上限、下限、、drm()names=c()drcdcED50ED50表示,最后是斜率,,绕ebED50ED50.
ryegrass.m1 <- drm(rootl ~ conc, data = ryegrass,
fct = LL.4(names = c("Slope", "Lower Limit", "Upper Limit", "ED50")))
summary(ryegrass.m1)
##
## Model fitted: Log-logistic (ED50 as parameter) (4 parms)
##
## Parameter estimates:
##
## Estimate Std. Error t-value p-value
## Slope:(Intercept) 2.98222 0.46506 6.4125 2.960e-06 ***
## Lower Limit:(Intercept) 0.48141 0.21219 2.2688 0.03451 *
## Upper Limit:(Intercept) 7.79296 0.18857 41.3272 < 2.2e-16 ***
## ED50:(Intercept) 3.05795 0.18573 16.4644 4.268e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error:
##
## 0.5196256 (20 degrees of freedom)
曲线拟合的摘要显示四个参数中每个参数的估计值及其标准误差。p 值告诉我们参数是否不同于零。在这种情况下,所有四个参数都与零明显不同,如图所示,对数逻辑曲线似乎非常适合数据。
op <- par(mfrow = c(1, 2), mar=c(3.2,3.2,.5,.5), mgp=c(2,.7,0))
plot(ryegrass.m1, broken=TRUE, bty="l",
xlab="Concentration of Ferulic Acid", ylab="Length of Roots")
plot(ryegrass.m1, broken=TRUE, bty="l",
xlab="Concentration of Ferulic Acid", ylab="Length of Roots",type="all")
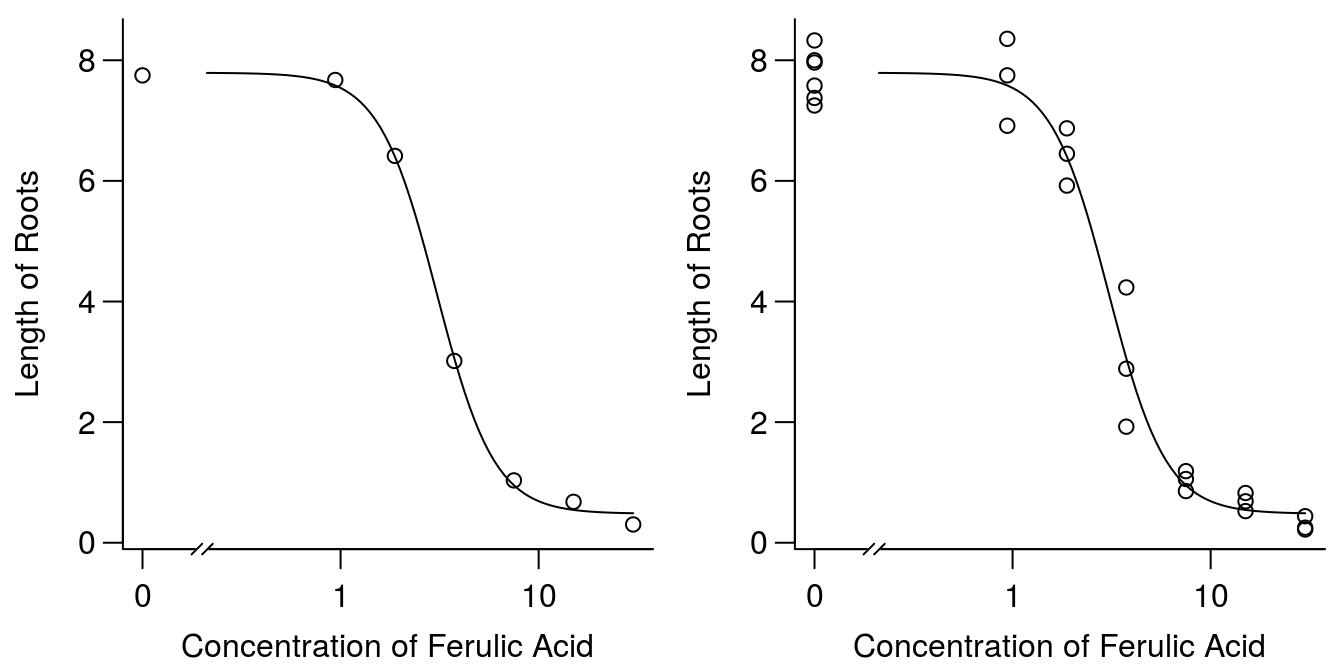
图 2:每个浓度(左)和所有观测值(右)的回归和观测值平均值图。
2. 更多剂量-反应曲线
在评估除草剂选择性时,一条剂量 – 反应曲线并不能告诉您任何事情。除草剂的选择性总是具有剂量依赖性的,并且具有预先固定收获日的生物测定只能提供除草剂效果的快照。在比较同一植物物种上的两种除草剂或两种植物物种上的一种除草剂的剂量 – 反应曲线时,您必须在同一时间点或至少接近并处于植物发育的同一阶段运行。包装中的训练数据集由两条剂量- 反应曲线组成,一条用于苯他松,另一条用于草甘膦。S.albadrc
head(S.alba,n=2)
## Dose Herbicide DryMatter
## 1 0 Glyphosate 4.7
## 2 0 Glyphosate 4.6
tail(S.alba,n=2)
## Dose Herbicide DryMatter
## 67 640 Bentazone 0.6
## 68 640 Bentazone 0.8
## Fitting a log-logistic model with
S.alba.m1 <- drm(DryMatter ~ Dose, Herbicide, data=S.alba, fct = LL.4())
请注意,变量除草剂标识除草剂,因此,其中的第三个参数是分类变量 。drm()Herbicide
modelFit(S.alba.m1)
## Lack-of-fit test
##
## ModelDf RSS Df F value p value
## ANOVA 53 8.0800
## DRC model 60 8.3479 7 0.2511 0.9696
summary(S.alba.m1)
##
## Model fitted: Log-logistic (ED50 as parameter) (4 parms)
##
## Parameter estimates:
##
## Estimate Std. Error t-value p-value
## b:Glyphosate 2.715409 0.748279 3.6289 0.0005897 ***
## b:Bentazone 5.134810 1.130949 4.5403 2.760e-05 ***
## c:Glyphosate 0.891238 0.194703 4.5774 2.421e-05 ***
## c:Bentazone 0.681845 0.095111 7.1689 1.288e-09 ***
## d:Glyphosate 3.875759 0.107463 36.0661 < 2.2e-16 ***
## d:Bentazone 3.805791 0.110341 34.4911 < 2.2e-16 ***
## e:Glyphosate 62.087606 6.611444 9.3909 2.184e-13 ***
## e:Bentazone 29.268444 2.237090 13.0833 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error:
##
## 0.3730047 (60 degrees of freedom)
缺乏拟合的检验显示无意义,此外,摘要显示上限 s 彼此非常接近,同样适用于下限 s。因此,我们可以考虑它们在两条曲线上是相似的。我们使用函数中的参数使两条曲线的上限和下限相似。该参数遵循参数名称的字母顺序。下面,我们将允许参数在两种除草剂之间自由变化,而对于两种除草剂,参数将保持不变(它们具有相同的标识 )。最后,参数可以自由变化。
dcdrm()pmodels=data.frame(..)b,c,d,ebcd1,1e
## common lower and upper limits
S.alba.m2 <- drm(DryMatter ~ Dose, Herbicide, data=S.alba, fct = LL.4(),
pmodels=data.frame(Herbicide, 1, 1, Herbicide))
summary(S.alba.m2)
##
## Model fitted: Log-logistic (ED50 as parameter) (4 parms)
##
## Parameter estimates:
##
## Estimate Std. Error t-value p-value
## b:Bentazone 5.046141 1.040135 4.8514 8.616e-06 ***
## b:Glyphosate 2.390218 0.495959 4.8194 9.684e-06 ***
## c:(Intercept) 0.716559 0.089245 8.0291 3.523e-11 ***
## d:(Intercept) 3.854861 0.076255 50.5519 < 2.2e-16 ***
## e:Bentazone 28.632355 2.038098 14.0486 < 2.2e-16 ***
## e:Glyphosate 66.890545 5.968819 11.2067 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error:
##
## 0.3705151 (62 degrees of freedom)
par(mfrow=c(1,1), mar=c(3.2,3.2,.5,.5), mgp=c(2,.7,0))
plot(S.alba.m1, broken=TRUE, bty="l")
plot(S.alba.m2, col="red", broken=TRUE, add=TRUE, legend=FALSE)
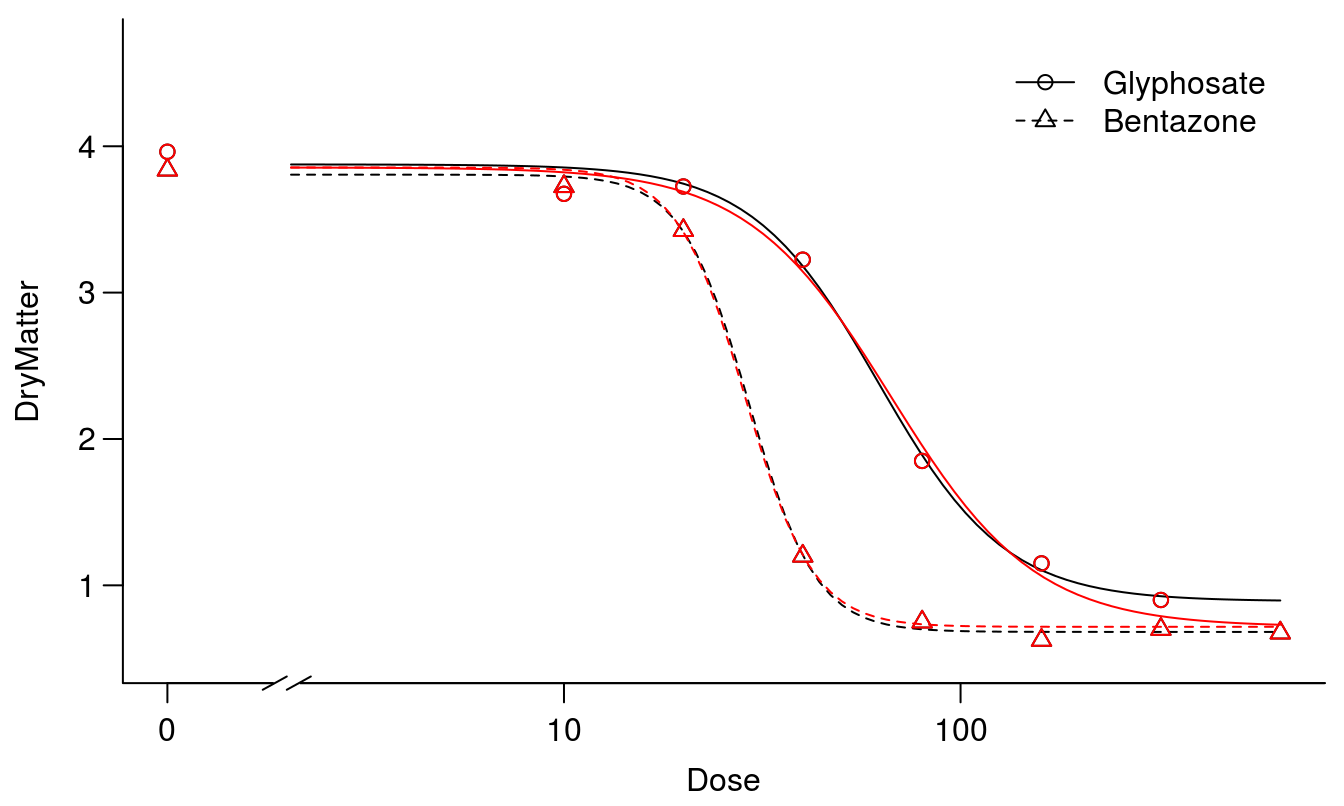
图3. 两个拟合,一个不假设两条曲线的公共上限和下限(黑色),另一条曲线具有相同的上限和下限(红色)。
anova(S.alba.m1, S.alba.m2) # Test for lack of fit not signifiancant
##
## 1st model
## fct: LL.4()
## pmodels: Herbicide, 1, 1, Herbicide
## 2nd model
## fct: LL.4()
## pmodels: Herbicide (for all parameters)
## ANOVA table
##
## ModelDf RSS Df F value p value
## 2nd model 62 8.5114
## 1st model 60 8.3479 2 0.5876 0.5588
请问怎么提取各个药剂EC50值呢