前言
NormqPCR这个包用于对qPCR数据进行均一化(normalization,这里需要注意的是,这里的normalization只是使用内参来校正目标基因的表达的意思,与统计学中的归一化(Normalization),中心化(center),标准化(scales)之类的术语没有关系)。这篇笔记主要是翻译了这个包的英文文档,本文档以一个小型案例(vignette)来演示了这个包的主要功能,笔记主要内容如下所示:
1. 合并技术重复(technical replicates)(了解即可);
2. 处理低Cq值(undetermined values)(了解即可);
3. 计算用于均一化的最佳管家基因(housekeeping genes)(这个最重要,其余的很多函数其实了解即可,这一部分要了解geNorm和NormFinder的算法原理);
4. 使用管家基因来对数据进行均一化(normalization)(了解)。
注:在这篇笔记中,管家基因(housekeeping genes)与内参(reference)指的是同一个意思。
由于原文档有点长,有一些东西了解一下就行,如果想要看完整的笔记,可以单击阅读原文直接看我博客的内容。公众号里只放第三部分内容(即如何计算最稳定的内参)。
选择最稳定内参基因
这一部分涉及选择最稳定的内参基因,其中用的是geNorm算法,这个算法的相关文献信息如下所示(后面会专门写这篇文献的阅读笔记):
Jo Vandesompele, Katleen De Preter, Filip Pattyn et al. (2002). Accurate normalization of real-time quantitative RT-PCR data by geometric averaging of multiple internal control genes. Genome Biology 2002. 3(7):research0034.1-0034.11. http://genomebiology.com/2002/3/7/research/0034/
geNorm方法
先加载数据,这里所用的数据都是前文提到的那篇文献里的数据,如下所示:
# BiocManager::install("ReadqPCR")
# BiocManager::install("NormqPCR")
# Following two packages is used to input raw data for qPCR
library(NormqPCR)
library(ReadqPCR)
options(width = 68)
data(geNorm)
str(exprs(geNorm.qPCRBatch))
数据结构如下所示:
> str(exprs(geNorm.qPCRBatch))
num [1:10, 1:85] 0.0425 0.0576 0.1547 0.1096 0.118 ...
- attr(*, "dimnames")=List of 2
..nbsp;: chr [1:10] "ACTB" "B2M" "GAPD" "HMBS" ...nbsp;: chr [1:85] "BM1" "BM2" "BM3" "BM4" ...
现在我们对选择的内参基因进行排序。我们在这里使用selectHKs()函数来实现geNorm算法中的逐步处理过程,这里的数据都是文献中材料与方法中提到的数据。
第一步,我们计算所有内参基因稳定检测值M后,排除那些M值最高的内参基因;
第二步,再次计算M值,再排除掉最高M值的内参基因,直到剩下两个内参基因(也就是参数minNrHK=2,如下所示:
tissue <- as.factor(c(rep("BM", 9), rep("FIB", 20), rep("LEU", 13),rep("NB", 34), rep("POOL", 9)))
res.BM <- selectHKs(geNorm.qPCRBatch[,tissue == "BM"], method = "geNorm",Symbols = featureNames(geNorm.qPCRBatch),minNrHK = 2, log = FALSE)
计算过程中,这个函数会给出不断计算的M值,结果如下所示:
res.BM <- selectHKs(geNorm.qPCRBatch[,tissue == "BM"], method = "geNorm",Symbols = featureNames(geNorm.qPCRBatch),minNrHK = 2, log = FALSE)
###############################################################
Step 1:
stability values M:
HPRT1 YWHAZ RPL13A UBC GAPD SDHA TBP
0.5160313 0.5314564 0.5335963 0.5700961 0.6064919 0.6201470 0.6397969
HMBS B2M ACTB
0.7206013 0.7747634 0.8498739
average stability M: 0.63628545246682
variable with lowest stability (largest M value): ACTB
Pairwise variation, (9/10): 0.0764690052563778
###############################################################
Step 2:
stability values M:
HPRT1 RPL13A YWHAZ UBC GAPD SDHA TBP
0.4705664 0.5141375 0.5271169 0.5554718 0.5575295 0.5738460 0.6042110
HMBS B2M
0.6759176 0.7671985
average stability M: 0.582888329316757
variable with lowest stability (largest M value): B2M
Pairwise variation, (8/9): 0.0776534266912183
###############################################################
Step 3:
stability values M:
HPRT1 RPL13A SDHA YWHAZ UBC GAPD TBP
0.4391222 0.4733732 0.5243665 0.5253471 0.5403137 0.5560120 0.5622094
HMBS
0.6210820
average stability M: 0.530228279613623
variable with lowest stability (largest M value): HMBS
Pairwise variation, (7/8): 0.0671119963410967
###############################################################
Step 4:
stability values M:
HPRT1 RPL13A YWHAZ UBC SDHA GAPD TBP
0.4389069 0.4696398 0.4879728 0.5043292 0.5178634 0.5245346 0.5563591
average stability M: 0.499943693933222
variable with lowest stability (largest M value): TBP
Pairwise variation, (6/7): 0.0681320232188603
###############################################################
Step 5:
stability values M:
HPRT1 RPL13A UBC YWHAZ GAPD SDHA
0.4292808 0.4447874 0.4594181 0.4728920 0.5012107 0.5566762
average stability M: 0.477377523800525
variable with lowest stability (largest M value): SDHA
Pairwise variation, (5/6): 0.0806194432580746
###############################################################
Step 6:
stability values M:
UBC RPL13A HPRT1 YWHAZ GAPD
0.4195958 0.4204997 0.4219179 0.4424631 0.4841646
average stability M: 0.437728198765878
variable with lowest stability (largest M value): GAPD
Pairwise variation, (4/5): 0.0841653121631615
###############################################################
Step 7:
stability values M:
RPL13A UBC YWHAZ HPRT1
0.3699163 0.3978736 0.4173706 0.4419220
average stability M: 0.406770625156432
variable with lowest stability (largest M value): HPRT1
Pairwise variation, (3/4): 0.097678269387021
###############################################################
Step 8:
stability values M:
UBC RPL13A YWHAZ
0.3559286 0.3761358 0.3827933
average stability M: 0.371619241507029
variable with lowest stability (largest M value): YWHAZ
Pairwise variation, (2/3): 0.113745049966055
###############################################################
Step 9:
stability values M:
RPL13A UBC
0.3492712 0.3492712
average stability M: 0.349271187472188
> res.BM
$ranking
1 1 3 4 5 6 7
"RPL13A" "UBC" "YWHAZ" "HPRT1" "GAPD" "SDHA" "TBP"
8 9 10
"HMBS" "B2M" "ACTB"
$variation
9/10 8/9 7/8 6/7 5/6 4/5
0.07646901 0.07765343 0.06711200 0.06813202 0.08061944 0.08416531
3/4 2/3
0.09767827 0.11374505
$meanM
10 9 8 7 6 5
0.6362855 0.5828883 0.5302283 0.4999437 0.4773775 0.4377282
4 3 2
0.4067706 0.3716192 0.3492712
以上只是BM这类组织的计算结果。现在我们把其它的组织都计算出来,如下所示:
res.POOL <- selectHKs(geNorm.qPCRBatch[,tissue == "POOL"],
method = "geNorm",
Symbols = featureNames(geNorm.qPCRBatch),
minNrHK = 2, trace = FALSE, log = FALSE)
res.FIB <- selectHKs(geNorm.qPCRBatch[,tissue == "FIB"],
method = "geNorm",
Symbols = featureNames(geNorm.qPCRBatch),
minNrHK = 2, trace = FALSE, log = FALSE)
res.LEU <- selectHKs(geNorm.qPCRBatch[,tissue == "LEU"],
method = "geNorm",
Symbols = featureNames(geNorm.qPCRBatch),
minNrHK = 2, trace = FALSE, log = FALSE)
res.NB <- selectHKs(geNorm.qPCRBatch[,tissue == "NB"],
method = "geNorm",
Symbols = featureNames(geNorm.qPCRBatch),
minNrHK = 2, trace = FALSE, log = FALSE)
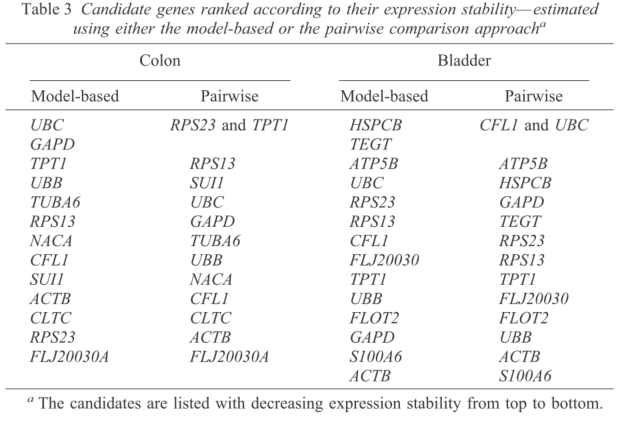
我们就获得了基因的下面排序信息,这个就是文献中的Table 3,文献中的信息如下所示:
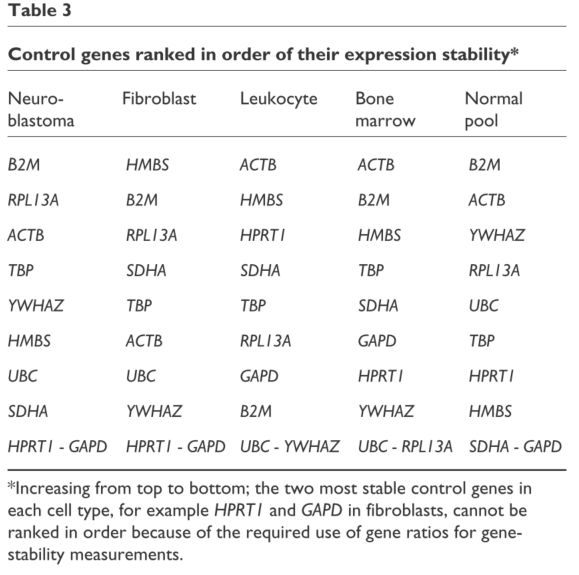
我们自己的计算结果:
ranks <- data.frame(c(1, 1:9),
res.BM$ranking, res.POOL$ranking,
res.FIB$ranking, res.LEU$ranking,
res.NB$ranking)
names(ranks) <- c("rank", "BM", "POOL", "FIB", "LEU", "NB")
ranks
结果如下所示:
ranks
rank BM POOL FIB LEU NB
1 1 RPL13A GAPD GAPD UBC GAPD
2 1 UBC SDHA HPRT1 YWHAZ HPRT1
3 2 YWHAZ HMBS YWHAZ B2M SDHA
4 3 HPRT1 HPRT1 UBC GAPD UBC
5 4 GAPD TBP ACTB RPL13A HMBS
6 5 SDHA UBC TBP TBP YWHAZ
7 6 TBP RPL13A SDHA SDHA TBP
8 7 HMBS YWHAZ RPL13A HPRT1 ACTB
9 8 B2M ACTB B2M HMBS RPL13A
10 9 ACTB B2M HMBS ACTB B2M
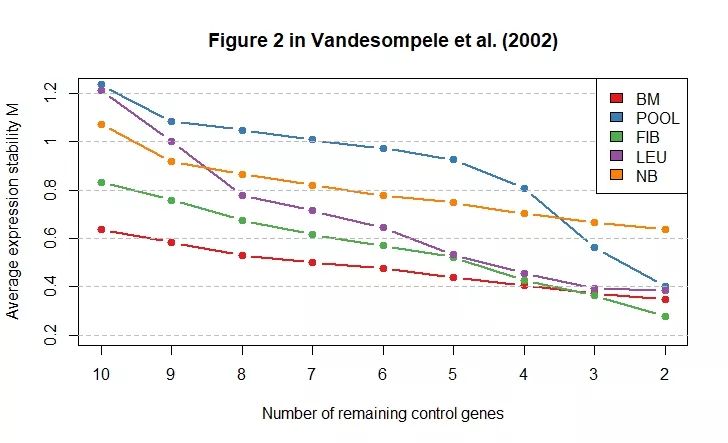
现在绘制出每个细胞类型的平均基因表达稳定值M的折线图,这个对应于文献中的Figure 2,如下所示:
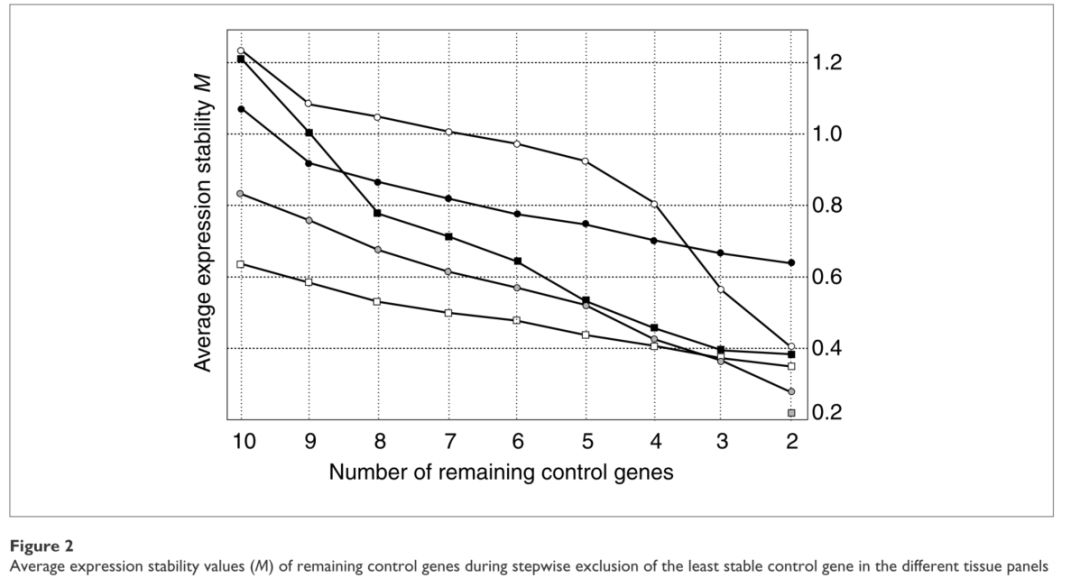
代码如下所示:
library(RColorBrewer)
mypalette <- brewer.pal(5, "Set1")
matplot(cbind(res.BM$meanM, res.POOL$meanM, res.FIB$meanM,
res.LEU$meanM, res.NB$meanM), type = "b",
ylab = "Average expression stability M",
xlab = "Number of remaining control genes",
axes = FALSE, pch = 19, col = mypalette,
ylim = c(0.2, 1.22), lty = 1, lwd = 2,
main = "Figure 2 in Vandesompele et al. (2002)")
axis(1, at = 1:9, labels = as.character(10:2))
axis(2, at = seq(0.2, 1.2, by = 0.2), labels = seq(0.2, 1.2, by = 0.2))
box()
abline(h = seq(0.2, 1.2, by = 0.2), lty = 2, lwd = 1, col = "grey")
legend("topright", legend = c("BM", "POOL", "FIB", "LEU", "NB"),
fill = mypalette)
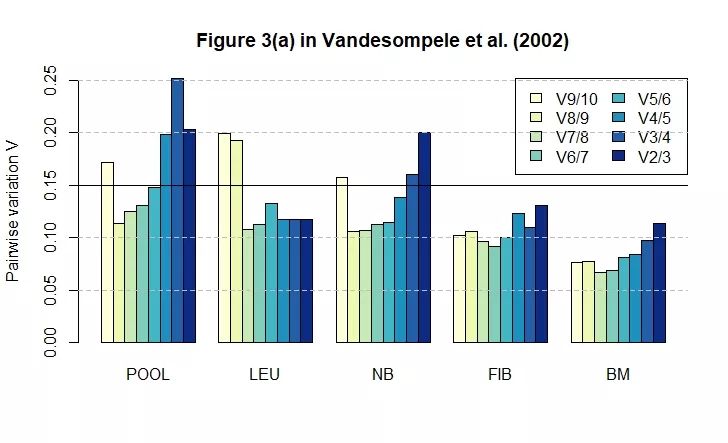
绘制每个细胞类型的成对方差(pairwise variation)图,这个对应文献中的Figure 3,如下所示:
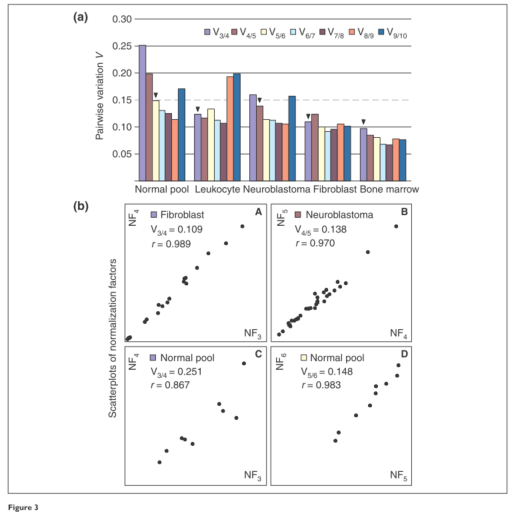
代码如下所示:
mypalette <- brewer.pal(8, "YlGnBu")
barplot(cbind(res.POOL$variation, res.LEU$variation, res.NB$variation,
res.FIB$variation, res.BM$variation), beside = TRUE,
col = mypalette, space = c(0, 2),
names.arg = c("POOL", "LEU", "NB", "FIB", "BM"),
ylab = "Pairwise variation V",
main = "Figure 3(a) in Vandesompele et al. (2002)")
legend("topright", legend = c("V9/10", "V8/9", "V7/8", "V6/7",
"V5/6", "V4/5", "V3/4", "V2/3"),
fill = mypalette, ncol = 2)
abline(h = seq(0.05, 0.25, by = 0.05), lty = 2, col = "grey")
abline(h = 0.15, lty = 1, col = "black")
注:文献中推荐的成对方差值的截止值为0.15,因此低于此值后,就不需要使用其它的内参基因了。
如何将自己的数据导入分析?
输入数据格式如下:Data
qPCRBatch <- read.qPCR(“Data路径”)
rownames(exprs(qPCRBatch))
res <- selectHKs(qPCRBatch, method = "geNorm",Symbols = featureNames(qPCRBatch),minNrHK = 2, log = FALSE)
rank<-res$ranking获得排名
NormFinder方法
第二种选择内参的基因的方法是NormFinder,这种方法来源于以下文献:
Andersen, C. L., et al. (2004). “Normalization of real-time quantitative reverse transcription-PCR data: a model-based variance estimation approach to identify genes suited for normalization, applied to bladder and colon cancer data sets.” Cancer Res 64(15): 5245-5250.
现在我们计算Table 3,如下所示:
第一步,导入数据::
## NormFinder
data(Colon)
Colon
结果如下所示:
> data(Colon)
> Colon
qPCRBatch (storageMode: lockedEnvironment)
assayData: 13 features, 40 samples
element names: exprs
protocolData: none
phenoData
sampleNames: I459N 90 ... I-C1056T (40 total)
varLabels: Sample.no. Classification
varMetadata: labelDescription
featureData
featureNames: UBC UBB ... TUBA6 (13 total)
fvarLabels: Symbol Gene.name
fvarMetadata: labelDescription
experimentData: use 'experimentData(object)'
Annotation: Table 1 in Andersen et al. (2004)
继续计算,如下所示:
Class <- pData(Colon)[,"Classification"]
res.Colon <- stabMeasureRho(Colon, group = Class, log = FALSE)
sort(res.Colon) # see Table 3 in Andersen et al (2004)
结果如下所示:
> sort(res.Colon) # see Table 3 in Andersen et al (2004)
UBC GAPD TPT1 UBB TUBA6 RPS13 NACA
0.1821707 0.2146061 0.2202956 0.2471573 0.2700641 0.2813039 0.2862397
CFL1 SUI1 ACTB CLTC RPS23 FLJ20030
0.2870467 0.3139404 0.3235918 0.3692880 0.3784909 0.3935173
再看另外的一个数据集Bladder,如下所示:
data(Bladder)
Bladder
grade <- pData(Bladder)[,"Grade"]
res.Bladder <- stabMeasureRho(Bladder,
group = grade,
log = FALSE)
sort(res.Bladder)
计算结果如下所示:
> data(Bladder)
> Bladder
qPCRBatch (storageMode: lockedEnvironment)
assayData: 14 features, 28 samples
element names: exprs
protocolData: none
phenoData
sampleNames: 335-6 1131-1 ... 1356-1 (28 total)
varLabels: Sample.no. Grade
varMetadata: labelDescription
featureData
featureNames: ATP5B HSPCB ... FLJ20030 (14 total)
fvarLabels: Symbol Gene.name
fvarMetadata: labelDescription
experimentData: use 'experimentData(object)'
Annotation: Table 1 in Andersen et al. (2004)
> grade <- pData(Bladder)[,"Grade"]
> res.Bladder <- stabMeasureRho(Bladder,
+ group = grade,
+ log = FALSE)
Warning message:
In .local(x, ...) : Argument 'group' is transformed to a factor vector.
> sort(res.Bladder)
HSPCB TEGT ATP5B UBC RPS23 RPS13 CFL1
0.1539598 0.1966556 0.1987227 0.2033477 0.2139626 0.2147852 0.2666129
FLJ20030 TPT1 UBB FLOT2 GAPD S100A6 ACTB
0.2672918 0.2691553 0.2826051 0.2960429 0.3408742 0.3453435 0.3497295
我们也可以使用geNorm算法来计算,如下所示:
selectHKs(Colon,
log = FALSE,
trace = FALSE,
Symbols = featureNames(Colon))$ranking
计算结果如下所示:
> selectHKs(Colon,
+ log = FALSE,
+ trace = FALSE,
+ Symbols = featureNames(Colon))$ranking
1 1 3 4 5 6 7
"RPS23" "TPT1" "RPS13" "SUI1" "UBC" "GAPD" "TUBA6"
8 9 10 11 12 13
"UBB" "NACA" "CFL1" "CLTC" "ACTB" "FLJ20030"
再来看Baldder的数据,如下所示:
selectHKs(Bladder,
log = FALSE,
trace = FALSE,
Symbols = featureNames(Bladder))$ranking
结果如下所示:
> selectHKs(Bladder,
+ log = FALSE,
+ trace = FALSE,
+ Symbols = featureNames(Bladder))$ranking
1 1 3 4 5 6 7
"CFL1" "UBC" "ATP5B" "HSPCB" "GAPD" "TEGT" "RPS23"
8 9 10 11 12 13 14
"RPS13" "TPT1" "FLJ20030" "FLOT2" "UBB" "ACTB" "S100A6"
我们也可以使用NormFinder算法的分步计算方式工来看多个内参基因的情况,也就是文献中附录中的Average control gene部分,selectHKs函数中含有这种算法的参数,如下所示:
Class <- pData(Colon)[,"Classification"]
selectHKs(Colon,
group = Class,
log = FALSE,
trace = TRUE,
Symbols = featureNames(Colon),
minNrHKs = 12,
method = "NormFinder")$ranking
结果如下所示:
> Class <- pData(Colon)[,"Classification"]
> selectHKs(Colon,
+ group = Class,
+ log = FALSE,
+ trace = TRUE,
+ Symbols = featureNames(Colon),
+ minNrHKs = 12,
+ method = "NormFinder")$ranking
###############################################################
Step 1:
stability values rho:
UBC GAPD TPT1 UBB TUBA6 RPS13 NACA
0.1821707 0.2146061 0.2202956 0.2471573 0.2700641 0.2813039 0.2862397
CFL1 SUI1 ACTB CLTC RPS23 FLJ20030
0.2870467 0.3139404 0.3235918 0.3692880 0.3784909 0.3935173
variable with highest stability (smallest rho value): UBC
###############################################################
Step 2:
stability values rho:
GAPD TPT1 UBB NACA CFL1 RPS13 TUBA6
0.1375298 0.1424519 0.1578360 0.1657364 0.1729069 0.1837057 0.1849021
SUI1 ACTB RPS23 FLJ20030 CLTC
0.2065531 0.2131651 0.2188277 0.2359623 0.2447588
variable with highest stability (smallest rho value): GAPD
###############################################################
Step 3:
stability values rho:
TPT1 NACA UBB RPS13 CFL1 TUBA6 FLJ20030
0.1108474 0.1299802 0.1356690 0.1411173 0.1474242 0.1532953 0.1583031
SUI1 ACTB RPS23 CLTC
0.1586250 0.1682972 0.1686139 0.1926907
variable with highest stability (smallest rho value): TPT1
###############################################################
Step 4:
stability values rho:
UBB TUBA6 ACTB CFL1 RPS13 SUI1 CLTC
0.09656546 0.09674897 0.10753445 0.10830099 0.11801680 0.12612399 0.12773131
NACA FLJ20030 RPS23
0.13422958 0.14609897 0.16530522
variable with highest stability (smallest rho value): UBB
###############################################################
Step 5:
stability values rho:
RPS13 SUI1 TUBA6 NACA FLJ20030 CFL1 ACTB
0.09085973 0.09647829 0.09943424 0.10288912 0.11097074 0.11428399 0.11495336
RPS23 CLTC
0.12635109 0.13286210
variable with highest stability (smallest rho value): RPS13
###############################################################
Step 6:
stability values rho:
ACTB TUBA6 CFL1 FLJ20030 NACA CLTC SUI1
0.09215478 0.09499893 0.09674032 0.10528784 0.10718604 0.10879846 0.11368091
RPS23
0.13134766
variable with highest stability (smallest rho value): ACTB
###############################################################
Step 7:
stability values rho:
SUI1 NACA FLJ20030 RPS23 TUBA6 CFL1 CLTC
0.08281504 0.08444905 0.08922236 0.09072667 0.10559279 0.10993755 0.13142181
variable with highest stability (smallest rho value): SUI1
###############################################################
Step 8:
stability values rho:
NACA CFL1 TUBA6 FLJ20030 CLTC RPS23
0.08336046 0.08410148 0.09315528 0.09775742 0.10499056 0.10554332
variable with highest stability (smallest rho value): NACA
###############################################################
Step 9:
stability values rho:
CFL1 TUBA6 CLTC FLJ20030 RPS23
0.07222968 0.07722737 0.08440691 0.09831958 0.12735605
variable with highest stability (smallest rho value): CFL1
###############################################################
Step 10:
stability values rho:
FLJ20030 TUBA6 CLTC RPS23
0.08162006 0.08189011 0.10705192 0.11430674
variable with highest stability (smallest rho value): FLJ20030
###############################################################
Step 11:
stability values rho:
TUBA6 CLTC RPS23
0.06978897 0.08069582 0.13702726
variable with highest stability (smallest rho value): TUBA6
###############################################################
Step 12:
stability values rho:
CLTC RPS23
0.1199009 0.1245241
variable with highest stability (smallest rho value): CLTC
1 2 3 4 5 6 7
"UBC" "GAPD" "TPT1" "UBB" "RPS13" "ACTB" "SUI1"
8 9 10 11 12
"NACA" "CFL1" "FLJ20030" "TUBA6" "CLTC"
Warning message:
In .local(x, ...) : Argument 'group' is transformed to a factor vector.
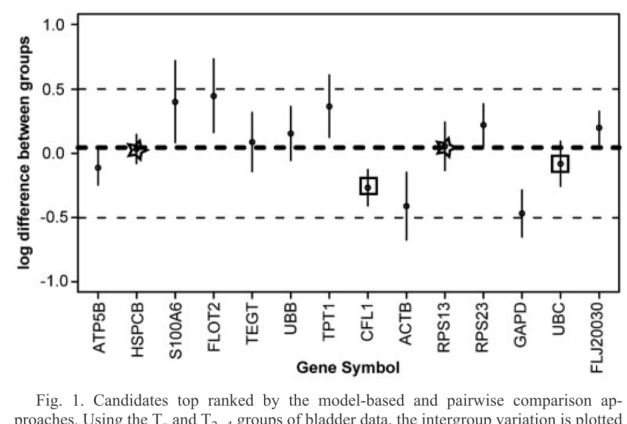
在Bladder数据集中,我们发现,排列前面的2个内参基因是HSPCB与RPS13,也就是Figure 1中的内容,如下所示:
grade <- pData(Bladder)[,"Grade"]
selectHKs(Bladder,
group = grade,
log = FALSE,
trace = FALSE,
Symbols = featureNames(Bladder),
minNrHKs = 13,
method = "NormFinder")$ranking
结果如下所示:
> grade <- pData(Bladder)[,"Grade"]
> selectHKs(Bladder,
+ group = grade,
+ log = FALSE,
+ trace = FALSE,
+ Symbols = featureNames(Bladder),
+ minNrHKs = 13,
+ method = "NormFinder")$ranking
1 2 3 4 5 6 7
"HSPCB" "RPS13" "UBC" "RPS23" "ATP5B" "TEGT" "UBB"
8 9 10 11 12 13
"FLJ20030" "CFL1" "S100A6" "FLOT2" "ACTB" "TPT1"
参考资料
- NormqPCR: Functions for normalisation of RT-qPCR data
- 2.
您好,请问NormqPCR这个包怎么下载呀?
您好,这个包在biocmanager
so,用
BiocManager::install(“NormqPCR”)
请问加载数据集那里如何使用自己的数据分析?格式是什么样的呢
你好,包里面有demo data file,你可以加载看看数据格式